伯特兰-切比雪夫定理

伯特兰—切比雪夫定理说明：若整数n＞3，则至少存在一个质数p，符合n＜p＜2n−2。另一个稍弱说法是：对于所有大于1的整数n，至少存在一个质数p，符合n＜p＜2n。

该定理被约瑟·伯特兰（JosephBertrand）提出，由切比雪夫（Chebyshev）证明。

1845年约瑟·伯特兰提出了“伯特兰-切比雪夫定理”这个猜想。伯特兰验证了2至3×10^6之间的所有数。1850年切比雪夫证明了这个猜想。拉马努金给出较简单的证明，而保罗·艾狄胥则借二项式系数给出了另一个简单的证明。

引理1：设

为一自然数，

为一素数，则能整除

的

的最高幂次为:

，（

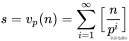
表示不大于

的最大整数）。

证明：能整除

的

的最高幂次显然等于从1到

的各自然数中

的最高幂次之和，即

(其中

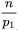
为能整除

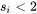
的

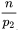
的最高幂次)。然后将从1到

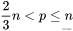
的所有(n个)自然数排列在一条直线上，在每个数字上叠放一列

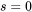
个记号，显然记号的总数是

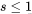
。关系式

表示的是先计算各列的记号数(即

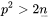
)再求和。但我们也可以先计算各行的记号数再求和，由此得到的关系式正是引理1。为了证明这一点，我们从数字所在的直线开始自下而上计数。很明显所有第一行有记号的数字都含有因子

(因为否则的话

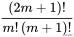
，没有记号)，这种数字的总数(也就是该行的记号总数)是

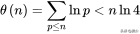
；第二行有记号的数字都含有因子(因为否则的话

，在第二行上不会有记号)，这种数字的总数(也就是该行的记号总数)是

，依此类推，第

行的记号总数为

。将所有这些数字相加便证明了引理1。（此段冗余应放入“勒让德定理”词条直接从推论1.1开始）

我们之所以用这样一种比较文字化的方式来叙述引理1的证明过程，目的在于更清楚地显示该证明的基本思路：即利用一个有限二维点阵求和的不同方式(顺序)得到互相等价的不同表达式。这是数学证明中一种常用的手段。

推论1.1：设n为一自然数，p为一素数，则能整除

的p的最高幂次为：

证明：显然。

推论1.2：设

为一自然数，p为一素数，s为能整除

的p的最高幂次，则：

(a)

；

(b)若

，则

；

(c)若

，则

。

证明：(a)设m为满足

的最大自然数，则显然对于i＞m，

。

因此推论1.1中的求和止于i=m，共计m项。由于

，

因此这m项中的每一项不是0就是1，其求和结果不超过项数本身，即

，

因此

。

(b)因为

表明

，因此由(a)可得

。

(c)因为

及

表明

，因此推论1.1中的求和只有

一项，即：

。由于

还表明

，因此s=2n/p-2n/p=2-2=0。

引理2：设n为自然数，p为素数，则Π(p≤n)p＜4^n。

证明：用数学归纳法。n=1和n=2时引理显然成立。

假设引理对n＜N成立(N＞2)，我们来证明n=N的情形。如果N为偶数，则

，引理显然成立。

如果N为奇数，设N=2m+1(m≥1)。注意到所有m+1＜p≤2m+1的素数都是组合数

的因子(因为它们是(2m+1)!的因子，但却不是m!和(m+1)!的因子)；另一方面组合数

在二项式展开(1+1)^(2m+1)中出现两次，因而

。

这两点合并可得

。由此(并利用归纳假定)可得

。

引理2常常被表述为

，并被称为Chebyshev'sBound(以Chebyshev命名的结果，无论是前面提到的Bertrand假设的别称Chebyshev定理还是这里所说的Chebyshev'sBound，都有不止一个对应，查阅文献时要当心)。

好了，一切准备就绪，然后我们来证明Bertrand假设。

Bertrand假设的证明：

用反证法，假设命题不成立，即存在某个n≥2，在n与2n之间没有素数。我们来看

的分解

(s(p)为质因子p的幂次)。由推论1.2(a)知p＜2n，由反证法假设知p≤n，再由推论1.2(c)知p≤2n/3，因此(2n)!/(n!n!)=Πp≤2n/3ps(p)。将连乘分解为p≤√2n及√2n＜p≤2n/3两部分(这一分解要求n＞4，但后面我们会看到，我们的整个方法只适用于n≥50，因此我们其实是假定n≥50，对50以下的情形只需直接验证即可)，并利用推论1.2(b)可得：

(2n)!/(n!n!)≤Πp≤√2nps(p)·Π√2np≤Πp≤√2nps(p)·Πp≤2n/3p

该乘积中的第一组的被乘因子数目为√2n以内的素数数目，即不多于√2n/2-1(因偶数及1不是素数)，而每个因子按照推论1.2(a)均不大于2n，因此该组乘积不大于(2n)√2n/2-1。第二组乘积按照引理2小于42n/3，由此得到：

(2n)!/(n!n!)＜(2n)√2n/2-1·42n/3。

另一方面，(2n)!/(n!n!)是(1+1)2n展开式中最大的一项，而该展开式共有2n项(我们将首末两项1合并为2)，因此(2n)!/(n!n!)≥22n/2n=4n/2n。将此式与上一段最后的结果联立并略经化简可得4n/3＜(2n)√n/2。两端取对数并进一步化简可得：

√2nln4＜3ln(2n)

由于幂函数√2n随n的增长速度远快于对数函数ln(2n)，因此上式对于足够大的n显然不可能成立。简单的数值计算表明，对于n=50上式左边为13.8629，右边为13.8155，不等式不成立。这表明我们所作的反证假设，即Bertrand假设不成立，对于n≥50是错误的，换句话说Bertrand假设对于n≥50成立。简单的验证可以证明Bertrand假设对于n＜50也成立(事实上前面说过，Bertrand本人就已经对n＜3000000做过验证)，因此我们证明了Bertrand假设。

Bertrand假设是一个非常简单的定理，本文所介绍的证明其基本思路在于显示当n与2n之间不存在素数时(2n)!/(n!n!)将无法找到足够多的素数因子来作分解，也就是说(2n)!/(n!n!)的素数分解表达式将小于(2n)!/(n!n!)，这就是上面不等式无法成立的原因。为什么选(2n)!/(n!n!)作为分析的对象？那是因为(2n)!/(n!n!)=(n+1)···(2n)/n!包含了所有n与2n之间的素数因子(分子上的(n+1)···(2n))，而又很聪明地约去了许多小于n的素数因子(分母上的n!)，因此非常适合于用来显示缺少了n与2n之间的素数所造成的后果。

Bertrand假设对素数分布作了非常粗略的描述，它表明在x附近的素数分布密度至少是1/x。与素数定理给出的1/ln(x)相比，Bertrand假设给出的显然很粗略(不过素数定理给出的密度是平均意义上的，而Bertrand假设给出的是严格的密度下界)，因而存在加强的余地。在本文的最后我们列举其中两个这样的加强结果(定理)：

定理1：对任意自然数n＞6，至少存在一个4k+1型和一个4k+3型素数p使得n＜p＜2n。

定理2：对任意自然数k，存在自然数N，对任意自然数n＞N至少存在k个素数p使得n＜p＜2n