几张反直觉的时空图，暴露出很多人根本不懂相对论

今天，我想谈一谈我们时空的形状究竟长什么样子，在本文中，我将尽可能忽略冗杂繁琐的数学推导过程，只留下那些对理解时空形状有帮助的结论。

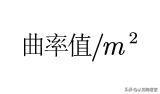
在少年时代，我们知道了加速度的存在，它无非就是：

而对于引力加速度：

如果仔细思考它，你会发现——引力加速度的产生只与距离r和天体质量M有关，同时它没有提到速度“v”。倘若我们对它求导数，就可以得到：（这里我故意用梯度符号，以表现“引力场”、“矢量场”的全局性质）

你问道：你对加速度求导是几个意思?

如果我们对这个导数除以光速c的平方，那么，我们将得到黎曼曲率标量R(有时候也叫高斯曲率（由于历史原因，两者转换需要乘以负二分之一）)：

rg为引力半径

黎曼曲率与所处环境以及所选择的坐标系无关，与选取的度规也无关。黎曼曲率反映了曲面自身的性质，它是一个内蕴不变量。它的量纲是什么？相信大家很好奇，它是:

简单理解，就是说我们取弯曲空间某局部的单位面积，它朝上长出来一个曲率值，这个值的绝对值越大，该局部空间向上凸或者向下凹的程度就越大。

黎曼（高斯）曲率的图像

什么是二维曲面和二维平面呢？在非欧几何中，我们不要认为弯曲的曲面有高度轴z，不要被它的“三维”表象所迷惑。弯曲的曲面是自然地延展开的，它不需要内嵌于三维空间中。

第一个图是二维的曲面，不要把它当做3维

你可以借助游乐场中凸面镜、凹面镜中的世界理解弯曲空间（但这和弯曲时空有根本区别，后面会提到）

哈哈镜

你无法把一张纸揉成一个球面（如果你硬揉，它就会褶皱破碎），同样，你无法把一个球展开成一张纸（如果你硬展，球就会裂成碎片）球的黎曼曲率是1/半径^2。而一张纸的黎曼曲率为0，对于时空，它生成的曲率为负，是双曲的。

即使是最简单的四维时空的几何，一个三维弯曲空间也需要用6个方向的黎曼张量分量才能描述，如果是更加复杂的模型，还需要引入挠率张量，扰动张量，甚至要考虑量子效应产生的对易关系。

这就是我为什么只选择静态史瓦西时空的「时-空」交织而成的「二维曲面」来间接描述时空的形状：

其实它只是（空间-空间）的二维曲面，这根本没有涉及到“时间”，因为它只是我们分析单纯的“空间度规”中的某种特殊情况得到的静态几何流形。这张图只是“长相充满艺术感”，同时又被某些科幻迷、媒体夸大其词，实则用处不大，和时间旅行也没什么关系（我的看法是宇宙的对称性不允许时间旅行）。

它满足这个曲线方程：

将其绕z轴旋转一周，就可以得到一个优美的旋转体：

下面这张示意图运用了夸张的艺术表现手法，它描述的正是“二维曲面”，同时它是双曲的，正如上文提到的黎曼曲率：

我们还要注意：这并不是空间（空-空）的形状，它其实是弯曲几何中的时间轴

和空间轴交织而成的时-空的形状。

时空曲率除了黑洞这样的极端天体外，它的值都很小。当r=rg时，任何物质无法逃逸出引力半径，当r趋于0时，时空曲率无穷大，也就是奇点所在的地方。对于空间曲率（空-空），它和时空曲率（时-空）有本质上的区别，最显然来看，空间曲率是正的，时空曲率是负的。

空间曲率是：

时空曲率在此基础上乘以负2。它们都是按照距离的三次方衰减的。

有些人说“引力导致了时空弯曲”，有些人说“引力只是弯曲时空的表现形式”。笔者对“谁是本质”的哲学争论丝毫不感兴趣。不过我相信，他们能认知宇宙本质的冰山几角。我只想说：“质量密度越大的地方，时空弯曲越厉害。时空弯曲越厉害的地方，质点所受的引力也越大。”

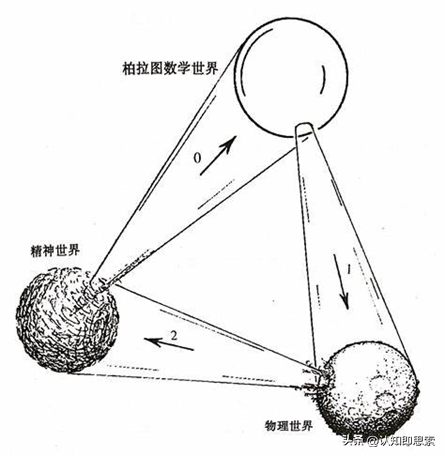
二维曲面和三维曲面的样子都可以直观地看出来（时-空的二维曲面并不存在于真实世界中，它是数学），然而四维时空（1维时间+三个空间维）长什么样子？这是不可想象的。不过它似乎虚假又真实地存在着。随便举个例子：彭罗斯认为现实的物理世界只是柏拉图精神宇宙的一个子集：

其实我在之前一篇总结性的文章中已经提过了那几个结论（而实际上广义相对论的强大远不止此）现在把它们拿出来看一下：

空间膨胀公式：

时间收缩公式：

对于地表低处的空间，高处的空间总是“收缩的”，高处的时间相对于低处的时间却是膨胀的。两者恰好相反。但差值依然是微乎其微。至于时间收缩和空间膨胀这两种实际效应，都能用时空曲率和空间曲率正向推导出来。

科学，正如其名，它不是万能的，不谈一个领域的适用范围就把它奉为一切事物的评判准则，那简直是耍流氓。科学存在着预言能力的「边界」，也就是存在着它所能认知范围的最大限度。

有些事情，我们不仅做不到，甚至想知道「为什么做不到」也做不到：非欧几何究竟意味着什么?数学难道不只是个形式工具吗？莫非时空真如存在主义、结构主义者们所认为的，是一种「高维流形」?数学究竟是某种客观实体还是虚无缥缈的形式工具?

这些谜团总是吸引着我们为之烦恼。「实验」和「观测」啊，倘若连你们都做不到，还有谁能做到？