小白入门编程之增量式，逐步优化，通用化编写方式

如果不是大牛，不能写出一步到位的代码，可以考虑增量式、逐步调试、逐步优化式编程。

即使是大牛，复杂的系统也是通过逐步更新版本迭代出来的，不是一步到位的。逐步更新的版本包括bug的修正，性能的优化，也包括功能的变更、增加。

1增量式，逐步调试，以打印九九乘法为例：

增量式是指功能不一步到位，逐步增加功能和代码量，逐步调试（一些规律大一点的程序要同时调试debug和release版），并尽量满足一些边界条件。

先写出框架：

(){for(inti=1;i=9;i++){for(intj=1;j=9;j++){printf("%d",i*j);}printf("\n");}while(1);//pausereturn0;}

运行效果：

挤成一堆了，改进一下：

printf("%d",i*j);//更改为printf("%5d",i*j);

运行效果：

右上角部分是多余的，去掉：

for(intj=1;j=9;j++){//更改为for(intj=1;j=i;j++){

运行效果：

将两个乘数添加上：

printf("%5d",i*j);//更改为printf("%d*%d=%4d",i,j,i*j);

运行效果：

积与等号隔得太远了，更改积的数字为左对齐，同时调整一下两个乘数的顺序：

printf("%d*%d=%-4d",i,j,i*j);

运行效果：

最终代码：

(intn){if(n2)returnfalse;//小于等于1的整数不可能是素数for(inti=2;in;i++){if(n%i==0)returnfalse;}returntrue;}intmain(){for(inti=0;i1000;i++)if(isPrime(i))printf("%3d\t",i);while(1){intn;printf("\n请输入一个整数：");scanf("%d",n);if(isPrime(n))printf("%disprime\n",n);elseprintf("%disnotprime\n",n);}return0;}

测试效果：

以上使用的是穷举法，考虑的优化就是要减少解空间。

如某一个数是否是素数的问题，只有奇数才可能是素数，偶数不是素数。

能被2整除的整数都不是素数（注意合适的搜索顺序）：

boolisPrime(intn){if(n2)returnfalse;//小于等于1的整数不是素数if(n==2)returntrue;//2是素数if(n%2==0)returnfalse;//除2以外，能被2整除的整数都不是素数for(inti=3;in;i+=2){if(n%i==0)returnfalse;}returntrue;}

并不需要穷举到n，设a*b=n，i*i=n，若a=i，则必有b=i。如8*8=64，则a如果是2、4、8，则b就是32、16、8，反过来也是如此，因此只需判定在2~√64之间有无因子即可。

intupper=sqrt(n)+1;for(inti=3;iupper;i+=2){if(n%i==0)returnfalse;}

完整代码：

(intn){if(n2)returnfalse;//小于等于1的整数不是素数if(n==2)returntrue;//2是素数if(n%2==0)returnfalse;//除2以外，能被2整除的整数都不是素数/**并不需要穷举到n，设a*b=n，i*i=n，若a=i，则必有b=i。*如8*8=64，则a如果是2、4、8，则b就是32、16、8，反过来也是如此，*因此只需判定在2~√64之间有无因子即可。*/intupper=sqrt(n)+1;for(inti=3;iupper;i+=2){if(n%i==0)returnfalse;}returntrue;}intmain(){for(inti=0;i1000;i++)if(isPrime(i))printf("%3d\t",i);while(1){intn;printf("\n请输入一个整数：");scanf("%d",n);if(isPrime(n))printf("%disprime\n",n);elseprintf("%disnotprime\n",n);}return0;}

从最简单的实例开始，逐步优化、通用化。

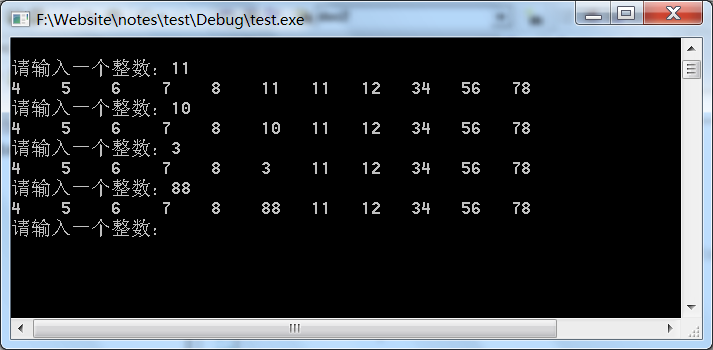
在一个已排序的数组中插入一个数，并保持有序。写出实例较简单和具体的代码：

(){restart:intdata[11]={4,5,6,7,8,11,12,34,56,78};//已排序数组，只有10个元素intinsert;//插入数intindex;//描写需要插入的位置printf("\n请输入一个整数：");scanf("%d",insert);if(insert=data[0])index=0;elseif(insert=data[9])index=10;else{for(inti=0;i10;i++)if(insert=data[i]insert=data[i+1]){index=i+1;break;}}for(intj=9;j=index;j--)data[j+1]=data[j];data[index]=insert;for(intk=0;k11;k++)printf("%-5d",data[k]);gotorestart;//循环测试一下return0;}

写成更通用的函数形式：

defineN11voidarrayInsert(intdata[],intinsert){intindex;//描写需要插入的位置if(insert=data[0])index=0;elseif(insert=data[N-2])index=N-1;else{for(inti=0;iN-2;i++)if(insert=data[i]insert=data[i+1]){index=i+1;break;}}for(intj=N-2;j=index;j--)data[j+1]=data[j];data[index]=insert;}intmain(){restart:staticintdata[N]={4,5,6,7,8,11,12,34,56,78};//已排序数组，10个值+1个0值intinsert;//插入数printf("\n请输入一个整数：");scanf("%d",insert);arrayInsert(data,insert);for(intk=0;kN;k++)printf("%-5d",data[k]);gotorestart;//循环测试一下，可考虑将数组设置为staticreturn0;}

4增量式，打印菱形图案

4.1打印上半部

//增量式，打印菱形图案(intn){for(inti=0;in;i++){for(intk=0;kn-i-1;k++)printf("");for(intj=0;j2*i-1;j++)//1,3,5,……printf("*");printf("\n");}for(i=1;in;i++){for(intk=0;ki;k++)printf("");for(intj=0;j2*(n-1)-2*i-1;j++)printf("*");printf("\n");}}intmain(){for(inti=3;i18;i++)dimond(i);while(1);//pausereturn0;}

可以用菱形图案来模拟杨辉三角：

(intn){int**arr=(int**)malloc(sizeof(int*)*n);for(inti=0;in;i++)arr[i]=(int*)malloc(sizeof(int)*n);for(i=0;in;i++){arr[i][0]=1;arr[i][i]=1;}for(i=2;in;i++){for(intj=1;ji;j++)arr[i][j]=arr[i-1][j-1]+arr[i-1][j];}for(i=0;in;i++){printf("%d",i);for(intk=0;k=n-i;k++)printf("");for(intj=0;j=i;j++)printf("%4d",arr[i][j]);printf("\n");}for(intj=0;jn;j++)free(arr[j]);free(arr);}intmain(){YangHui(12);return0;}

运行效果：

－－