每天学习一点：运算放大器中的频率补偿知识

本文我们将通过在PSpice中观察到的示例电路了解运算放大器频率补偿知识。

在本文中，我们将讨论运算放大器频率补偿及其在电路稳定性中的重要性。

如今，大多数运算放大器都通过合适的片上元件进行内部补偿。通常，补偿旨在用于闭环增益，一直到电压跟随器操作到达单位增益。运算放大器的子类可以补偿高于1的值的闭环增益，例如10V/V.它们被称为去补偿运算放大器（decompensatedop-amps），它们提供的动态比它们已被补偿的单位增益更快。（我们将在以后的文章中更深入地介绍这一概念。）

即使用户无法控制内部补偿，但对于更有效地运用运算放大器，必须具备对内部补偿的基本了解。

许多运算放大器包括：（1）提供差分增益的输入级，（2）提供额外增益的中间级，以及（3）提供功率驱动的输出级。沿着每级信号路径的节点的晶体管和寄生电容（straycapacitances）产生延迟，我们将它们集中在一起并与低通RC网络建模，如图1所示。（为简单起见，我们将忽略输出的延迟级因为它通常要快得多;在不需要电源驱动的片上系统中，这一级通常会被完全省略。）

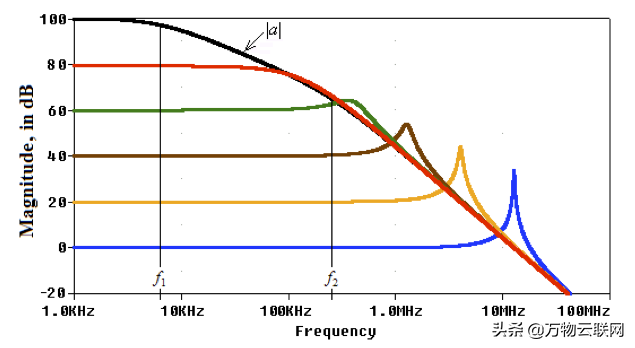
图1

图1.运算放大器的近似AC模型。

我们希望研究运算放大器的总增益a=Vo/Vd，也称为开环增益。在DC，所有电容器都用作开路，增益a取值：

公式1

在交流操作中，电路呈现两个极点频率，

公式2

图2

图2.用于绘制由R4确定的20-dB步长的闭环增益的PSpice电路。

公式3

并且将电路配置为非反相放大器，其理想情况是闭环增益Vo/Vi：

公式4

R4通过步进0,9kΩ，99kΩ，999kΩ和9,999kΩ的值会产生图3的闭环图（为方便起见，也显示了开环增益a的图示）。

图3

我们观察到，对于较大的Aideal值，AC响应相当平坦，但是对于较低的Aideal值，峰值量增加。但是我们应当注意到，因为1/β=Aideal，降低Aideal意味着降低1/β曲线，从而将交叉频率转移到|a|的曲线更陡斜率的区域。

由此导致的闭合速率（ROC，rate-of-closure）的增加降低了电路的相位裕度，从而引起不稳定性。（只有两个极点，我们的电路不会振荡，虽然它会在低增益时表现出无法忍受的峰值和振铃;但是，在我们的简化运算放大器模型中没有考虑的额外高频极点的存在可能会导致振荡的电路）。

很明显，最容易产生振荡的配置是单位增益电压跟随器，即β=1。如果运算放大器补偿了单位增益运算的足够相位裕度，那么它对所有其他闭环增益来说都是稳定的。

在图3的所有闭环增益中，由于没有峰值，最高增益（80dB）具有最佳轮廓。这是因为其交叉频率出现在ƒ1和ƒ2之间的中间频段，其中闭合率（ROC，rate-of-closure）约为20dB/dec，因此相位裕度约为90°。

我们也希望所有其他收益享有类似的相位差，一直到单位增益。这要求|a|曲线的整个斜率为-20dB/dec。因此，必须修改开环增益，使其轮廓由单极支配。

在下一篇文章中，我们将讨论通过并联电容实现此目的的一种方法。

在本文中，我们讨论了运算放大器频率补偿，并考虑了PSpice中的示例电路。在下一篇文章中，我们将介绍一种通过并联电容实现补偿的方法。